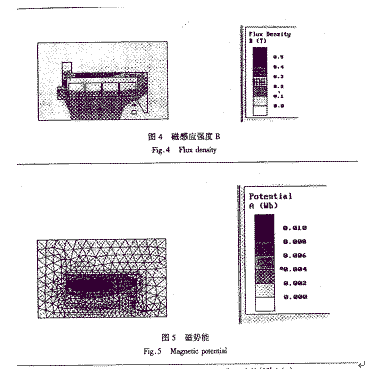
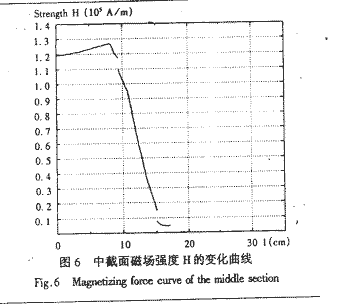
| 1. 引 言 磁选是利用不均匀磁场除去矿物中的磁性物质。在陶瓷行业中,原料中的铁质含量过高会影响瓷器的质量,因此磁选是陶瓷原料加工中的一道重要工序。不均匀磁场是磁选的必要条件,所谓不均匀磁场指磁场强度H和方向是变化的,可以是空间位置和时间的函数,一般用磁场梯度gradH表达不均匀性。矿粒在磁选中的单位质量所受磁场力(称比磁力)为: f磁=Khgradh,  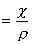 式中, f磁 为矿粒的比磁力,k为比磁化系数,χ为磁化系数, ρ为矿粒质量密度。 磁性矿粒在磁场力作用下运动,并被吸附到栅片上。目前磁选机设计计算过程中主要存在如下问题: 采用理论公式或经验公式计算磁场分布,铜耗大;由于磁选机磁路、边界条件较复杂,很难得到精确解。相反采用有限元方法可以获得较高精度的数值解。 1 磁场有限元分析原理 磁场有限元公式是基于Maxwell 方程组导出的,通过将标量势或矢量势引入Maxwell方程组并考虑其电磁性质关系,对二维静态的磁场分析,一般采用磁矢势法,其主自由度A只有一个,磁矢势的定义如下: B=�×A 式中,B为磁通密度,A为磁矢势,在二维问题中A只有一个分量。磁场有限元分析是先求出主自由度,然后通过有关公式求其它量,如对矢势公式两端进行面积分,并利用Stokes‘s公式就可求得磁通密度B和磁通量Φ: ∮cA• dl=∫sB•ds =Φ Maxwell 方程组是描述介质中的电场强度矢量E和磁场强度矢量H及电感应强度矢量D与磁感应强度矢量B的关系,由下列方程组表示: rotH= J + 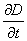 rotE=- rotE=- 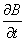 dirB=0, divD= dirB=0, divD=  式中,J为传导电流的体积密度,ρ为电荷体积密度。物质方程组为: D=εE, B= 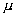 H, J= H, J= 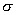 E E 式中,ε为介质介电常数,μ为磁导率,σ为电导率。可以引进矢量A和标势φ将问题的求解自由度降低,其中标势φ定义为: E+ 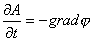 可以推导出用矢势和标势表达的电磁场方程(1)为: 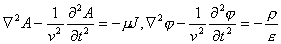 在静态电磁场中各物理量与时间无关,上式方程为: 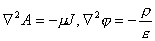 电磁场问题的边界条件一般有三类,即强制边界条件,自然边界条件,混合型边界条件。 对于平面电磁场问题,根据Maxwell方程,在具有一种介质的无源波导中,在定常状态下服从Helmholtz方程: 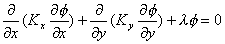 式中, φ可以为H分量或E分量,Kx= 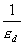 =Ky,λ=ω2μoε0,其中εd介质相对介电常数,μ0、ε0分别为自由空间的磁导率和介电常数,ω为波动频率。对磁场问题φ必须满足Neumann边界条件即 =Ky,λ=ω2μoε0,其中εd介质相对介电常数,μ0、ε0分别为自由空间的磁导率和介电常数,ω为波动频率。对磁场问题φ必须满足Neumann边界条件即 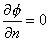 。将Helmholtz方程用泛函变分表示为: 。将Helmholtz方程用泛函变分表示为: 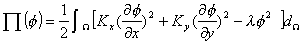 式中,Ω为二维积分域,使泛函Ⅱ(Ф)取极小场可建立有限元格式,采用三角形单元,其场变量模式可假设为:  ф(x,y)=α1+α2x+α3y 待定参数α1α2α3由三角形单元顶点的场变量 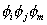 确定,Ф(x,y)可改为如下方程: 确定,Ф(x,y)可改为如下方程: Ф(x,y)=NIФI+NjФj+NmФm 式中,NI、Nj、Nm为形核函数: NI= 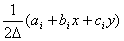 aI=xjym-xmyj bI=yj-ym cI=xm-xj 式中△三角形单元面积,将I换为j ,j换为m,m换为I ,就分别得到Nj1 Nm。 将空间域划分单元后,泛函Ⅱ(Ф)可表达为: Ⅱ(Ф)=∑Ⅱe(ф) ∑为区域中所有单元求和,对Ⅱ(ф)求极值可导出有限元方程式〔1〕: 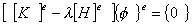 式中, 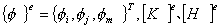 为单元系矩阵。对静态无源电磁场,有限元方程为: 为单元系矩阵。对静态无源电磁场,有限元方程为: 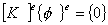 将各单元 将各单元 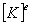 按“对号入座法”组集,可得到整体有限元方程,其有源静态电磁场整体有限元方程为(迭代格式): 按“对号入座法”组集,可得到整体有限元方程,其有源静态电磁场整体有限元方程为(迭代格式): 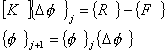 式中, 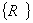 为电流、电压或永磁力载荷向量, 为电流、电压或永磁力载荷向量, 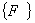 为剩余载荷向量,下标j为迭代次数。 为剩余载荷向量,下标j为迭代次数。 3。陶瓷泥浆间歇式磁选机磁场特性和有限元分析 本文分析的是螺线管(无铁心)磁系,分选腔上部和下部,由铸钢材料制成铁轭,线包由扁铜线绕制而成,共四组,每组之间由6mm厚的垫木承,分选腔采用铝质材料与线包隔离,工作气隙为2mm ,分选腔聚磁介质采用A3钢镀锌栅片。采用直流励磁,螺线管磁系的轴线中点磁场强度作为计算值,对于轴线较长的螺线管有理论公式计算磁场强度,但是对于多个线包,外面还有铁轭、磁极头等比较复杂的情况下采用理论公式计算就有误差,对漏磁、磁势能等也难以用理论公式计算。本文分析的磁选机主要参数如下:线包内径180mm,外径300mm,高度260mm电流密度为2.67A/mm2,背景磁场强度(空腔测试)1500Oe。 3.1有限元模型 采用轴对称模型,对磁选机对称部分建模用三角形单元,在工作气隙、磁极头处采用较细的网格,特别是在磁极头拐角位置需设置细网格,将铜、铝等不导磁材料的相对磁导率μr近似作为1处理,为了反映漏磁情况,将磁选机周围空气取一定的的半径建模并划分网格,在较远的位置处网格可以粗一些,将线圈的横截面(矩形)定义为块,输入电流密度值,该电流是励磁源电流,相当于电流载荷项。建模中需定义模型的边界条件,本模型将周围空气边界定义Dirichlet边界条件。电磁场有限元模型根据实际情况还可以定义为Neumann边界条件和法向磁感应强度为零的边界条件。本文分析的磁选机有限元模型共有459个结点,图1是有限元模型网格图。 3.2 计算结果分析和讨论 图2是磁力分布图。从图中看出,在铁轭处有较密的磁力线,磁力线在中部几乎与轴线平行,漏磁较少。 图3是合成磁场强度H的分布,在轴线和下磁极头有较高的值,并且变化剧烈,表明有较高的磁场梯度。图4是磁感应强度B。 图5为磁势能分布图,在铜导体内有较大的磁势能。图6是磁选机中截面磁场强度H的变化曲线,该曲线反映了磁场强度和其变化,在曲线的断开和陡峭的部分表明磁场梯度较大。 通过对湿式磁选机有限元模型分析的结果,我们知道磁场强度在分选腔中轴线各点,以及轴线任一断面的分布。另外,我们也能知道磁场梯度在分选腔中各处的大小,这些分析结果对提高陶瓷泥浆间隙式磁选机的磁分离效率是极为重要的。 本文分析尚未涉及分选腔中的聚磁介质,由于栅片特点,应作为周期对称模型,但分析时可取栅片局部,在周围加上外部磁场,可比较精确得到栅片局部的磁场分布,这一部分工作有待进一步完成。 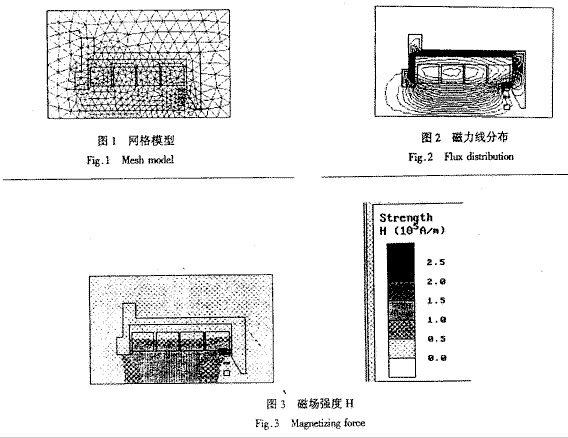
4 结 论 陶瓷泥浆间歇式磁选机的设计计算一般包括以下内容:确定螺线管的几何尺寸,计算使一定规格的螺线管达到预定的场强时所需的激磁功率;选择导线规格,计算螺线的匝数、安匝数、导线长度和重量,校核充填系数和功率;计算激磁电流和电压;选择冷却方案,计算冷却水的流量和线圈温升;确定铁铠磁路的断面积和材料等。 目前采用螺线管磁系的磁选机,一般螺线管外部用铁壳加以铠装。其目的在于减小磁路磁阻,增加螺线管内部场强。降低螺线管功率,理论可证明,螺线管铠装后功率可以降低一半。由于功率与场强的平方成正比,螺线管铠装后如保持原功率不变,则场强可以增大  倍 倍 从有限元分析结果来看,其磁力线分布与实际情况分布吻合。从理论公式计算出轴线中点为最大磁场强度。但由于铁铠形状复杂,加之磁选机线圈螺线管不属于长型螺线管,因此实际磁场强度最大值位置偏离轴线(参见图6)。利用有限元方法可以方便我们改变铁铠,磁极头形状、结构和尺寸,以得到最大磁场强度和磁场梯度在分选腔中的合理分布。并为找到最优磁选机尺寸、材料参数,节省铜耗等提供有效的设计计算依据和方法。 参考文献 1曾余庚等编著,电磁场有限单元法,北京;科学出版社,1982 2袁楚雄等编著,特殊选矿,北京:中国建筑工业出版社,1981
|

